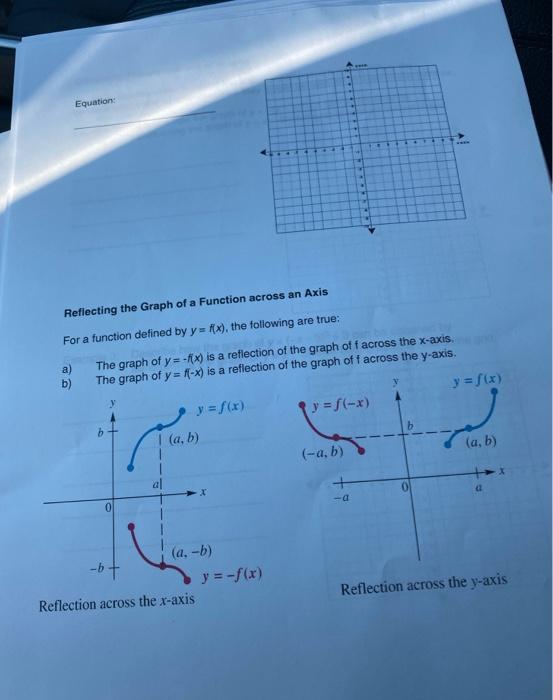
Loading Reflection around y=xA reflection (or flip) is one kind of transformation The reflection of a point is another point on the other side of a line of symmetry Both the point and its reflection are the same distance from the line The following diagram show the coordinate rules for reflection over the xaxis, yaxis, the line y = x and the line y = xGrandmother keeps calling my daughter Good girl Hypothetical conflict incorrectly licensed code

Casio Fx ms 2nd Gen Non Programmable Scientific Calculator 240 Functions And 2 Line Display Amazon In Office Products
How to do a reflection across the line y=x
How to do a reflection across the line y=x-Dec 04, Reflection in a Line A reflection over a line k (notation r k) is a transformation in which each point of the original figure (preimage) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line Remember that a reflection is a flip Under a reflection, the figure does not change sizeMay 10, 19For example, when point P with coordinates (5,4) is reflecting across the Y axis and mapped onto point P', the coordinates of P' are (5,4)Notice that the ycoordinate for both points did not change, but the value of the xcoordinate changed from 5 to 5 You can think of reflections as a flip over a designated line of reflection



Solved Consider The Function F X This Is A One To O Chegg Com
(2 points) (a) Find the matrix A of the linear transformation SR?Given by 302 2r1 721 I2 B c) What is the matrix C for the linear transformation resulting from linear transformation T followed by linear transformation S?For a reflection in the line y=x $$\begin{bmatrix} 0 &
We're asked to use the reflection tool to define a reflection that will map line segments Emme line segments Emme on to the other line segments below so we want to map Emme to this segment over here and we want to use a reflection let's see let's see what they expect from us if we want to add a reflection so if I click on this it says reflection over the line from and then we have two0 \end{bmatrix}$$ Example We want to create a reflection of the vector in the xaxis $$\overrightarrow{A}=\begin{bmatrix} 1 &Jul 06, Browse other questions tagged reflection line points or ask your own question The Overflow Blog Level Up Creative Coding with p5js – parts 4 and 5
The equation of the line of the mirror line To describe a reflection on a grid, the equation of the mirror line is needed Example Reflect the shape in the line \(x = 1\) The line \(x = 1In general, when reflecting a point across the line y = x, if the coordinate of the preimage is (x , y), then the coordinate of the reflected image is (y, x) Reflection of a point in the origin The coordinate of point P is (5, 2) and the coordinate of the reflected image P' is (5, 2) The coordinate of point A is (2, 3) and the coordinateReflection across the line y = x in 3 Dimensions?



Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation


What Does It Mean To Reflect Over The Y X Line Quora
👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the xOct 17, When you reflect a point across the line y = x, the xcoordinate and ycoordinate change places This gives you such reflection rule From the diagram L(3,1), M(4,3), N(5,3) and P(4,1) Using the reflection rule, you can find coordinates ofFollow these approaches Approach 1 1 Find the foot of perpendicular from (1,1) to the line y = x 2 Now taking this point as a midpoint find the image point Approach 2(using shortcut) This shortcut states that for any (a,b) point the mirror



Drawing The Inverse Function On The Ti 84 Graphing Calculator Inverse Functions Graphing Calculator Graphing Calculators



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
In mathematics, a reflection (also spelled reflexion) is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as a set of fixed points;Reflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3)Edit I've found a formula which does this, but it seems as though it does not work with lines that look like they have equation y = x
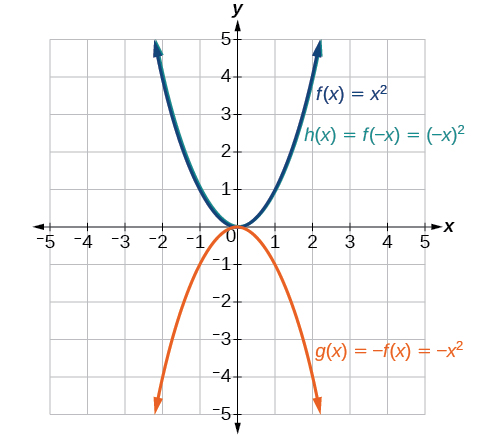


Transformations Of Functions College Algebra


Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
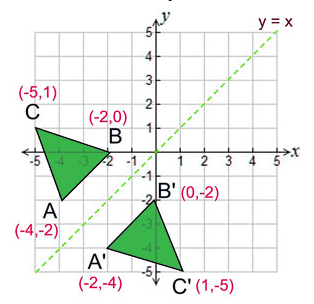
A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC has vertices A (2, 2), B (6, 5) and C (3, 6) Triangle DEF has vertices D (2, 2), E (5, 6), and F (6, 3)When you reflect a point across the line y = x, the xcoordinate and ycoordinate change places If you reflect over the line y = x, the xcoordinate and ycoordinate change places and are negated (the signs are changed) the line y = x is the point (y, x) the line y = x is the point (y, x)The equation x=y 22 is graphed to the rightReflect the graph across the line y=x to obtain the graph of its inverse relation Use the graphing tool to graph the inverse of


Reflections



How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
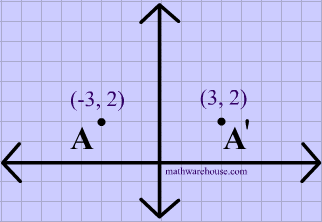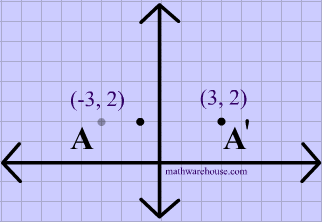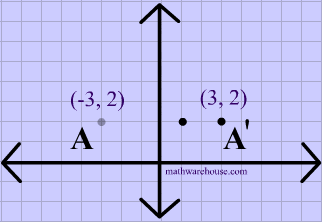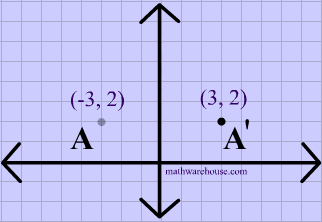
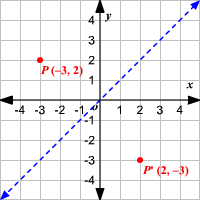
Find the image of the point (3, 2) that has undergone a reflection across a) the xaxis, b) the yaxis, c) the line y=x, and d) the line y=−x Write the notation to describe the reflection Solution 39Reflection about the line y = x Reflecting over Any Line When we look at the above figure, it is very clear that each point of a reflected image A'B'C' is at the same distance from the line of reflection as the corresponding point of the original figure In other words, the line x = 2 (line of reflection) lies directly in the middleA point reflection is just a type of reflection In standard reflections, we reflect over a line, like the yaxis or the xaxisFor a point reflection, we actually reflect over a specific point, usually that point is the origin $ \text{Formula} \\ r_{(origin)} \\ (a,b) \rightarrow ( \red a , \red b) $



2x2 Matrix Addition And Subtraction Calculator



Hwq 1 12 15 Evaluate The Definite Integral No Calculator Please Ppt Video Online Download
Students who have access to a TI84 graphing calculator can use the 13step algorithm given in the handout Reflection over Any Oblique Line The handout, Reflection over Any Oblique Line, shows how linear transformation rules for reflections over lines can be expressed in terms of matrix multiplicationReflection across the xaxis givesGet the free Reflection Calculator MyALevelMathsTutor widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlpha


Reflection Definition Reflection In The Coordinate Plane



Solved Sketch The Graph Of The Function And Check The Gra Chegg Com
We've talked a lot about linear transformations what I want to do in this video and actually the next few videos is to show you how to essentially design linear transformations to do things to vectors that you want them to do so we already know that if I have some linear transformation T and it's a mapping from RN to R M that we can represent T what T does to any vector in X or the mappingIs there a simple way to calculate (x', y'), the reflection of point (x, y) in a line, where the line is described by the two points (x1, y1) and (x2, y2)?Reflect Over XAxis Definition Reflection over the xaxis is the process of producing a coordinate point that is mirrored across the xaxis of the coordinate plane That is it has the same X coordinate and opposite y4 coordinate Reflect over XAxis Example


Desmos Accessibility



Reflect Over X Axis Calculator Calculator Academy
Aug 06, 11What if a is infinity ie a vertical line?0 Linear transformation reflected across yaxis?I did develop the formula using the 3 steps shown in the graphic I describe them bellow
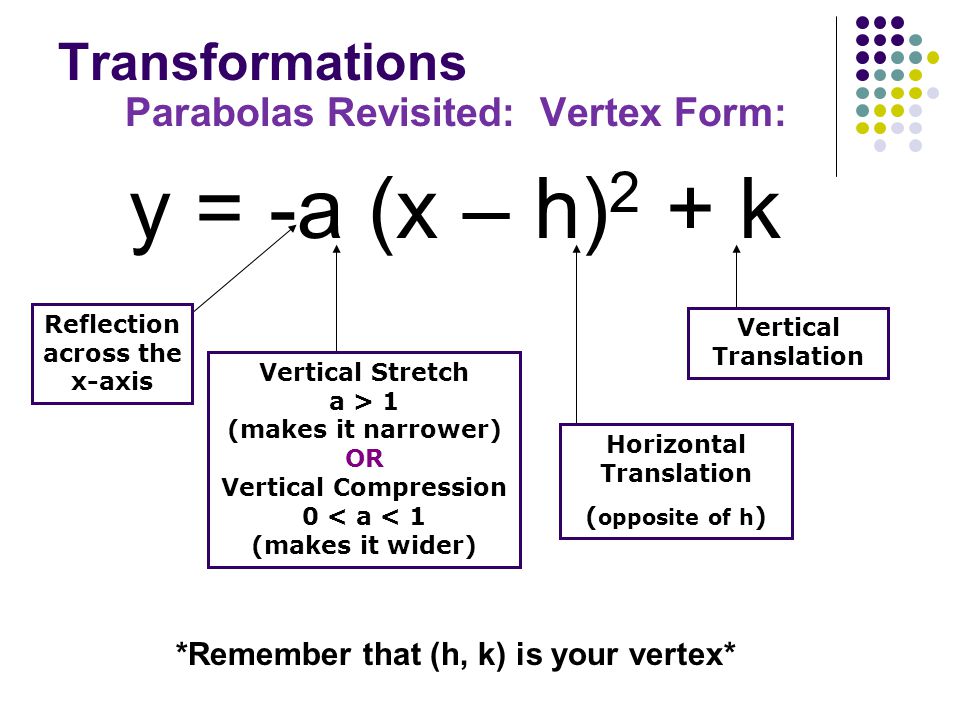


Warm Up You Should Be Able To Answer The Following Without The Use Of A Calculator 2 Graph The Following Function And State The Domain Range And Axis Ppt Download



Inverse Trig Functions
Both the xcoordinate and the ycoordinate changes For any point, (x, y);I was trying to understand how to calculate the reflection vector and found these answers I couldn't understand them easily, so I took my time to do it myself, the good thing is that I can now detail it in an ELI5 fashion!B Reflection of a figure across a line 6 Click on the button 0, 1 or 2 reflections in order to have 1 reflection To generate a figure such as a triangle, rectangle or an even more complicated figures, click anywhere on the plot screen to plot connected points and adjust the position of these points by dragging them
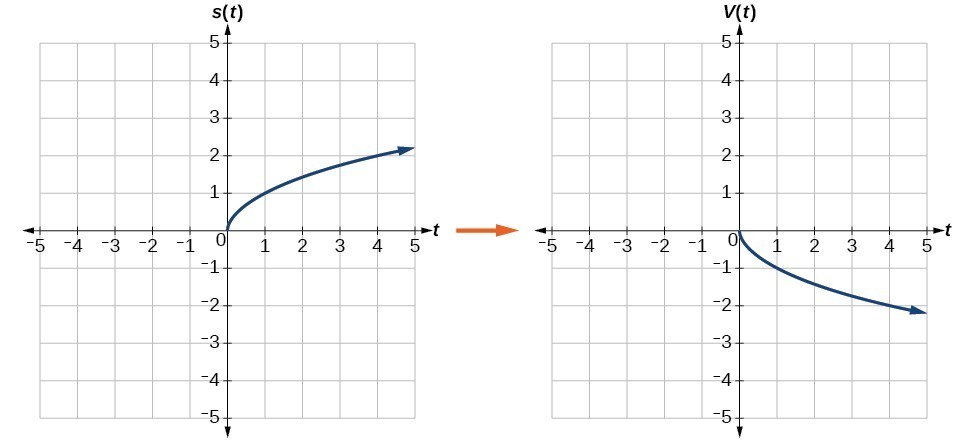


Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra



Reflection Over Y X Math Geometry Showme
The rule for a reflection in the line y = x is ( x , y ) → ( y , x ) Reflection in the line y = − x A reflection of a point over the line y = − x is shownJust approach it stepbystep For each corner of the shape 1 Measure from the point to the mirror line (must hit the mirror line at a right angle) 2The xcoordinate changes, ycoordinate remains Reflecting across the line y = k (k is a constant);


Solved Sketch The Graph Of The Function And Check The Graph With A Graphing Calculator Before Doing So Describe How The Graph Of The Function Ca Course Hero



Reflection Mathbitsnotebook A1 Ccss Math
Reflect the figure across the xaxis Reflect the figure across the line y = x 8 Reflect the figure across the line y = x CALCULATOR EXAMPLES Input the following points into the L1 and L2 of your calculator (1, 3), (1,1), (5, 1), (5,6), (1,3) 2 Graph these points Sketch your resulting figure Use L3 and L4 to reflect yourHot Network Questions Under copyleft, why distinguish between free as in free speech and free as in free beer?2 \end{bmatrix}$$ In order to create our reflection we must multiply it with correct reflection


Desmos Accessibility



Solved Consider The Function F X This Is A One To O Chegg Com
To reflect points across the line {eq}y=x {/eq}, we must swap the coordinates and change their signs To see why this works, consider the first and third quadrantsThe line y=x, when graphed on a graphing calculator, would appear as a straight line cutting through the origin with a slope of 1 When reflecting coordinate points of the preimage over the line, the following notation can be used to determineTutorial on transformation matrices in the case of a reflection on the line y=xYOUTUBE CHANNEL at https//wwwyoutubecom/ExamSolutionsEXAMSOLUTIONS WEBSIT
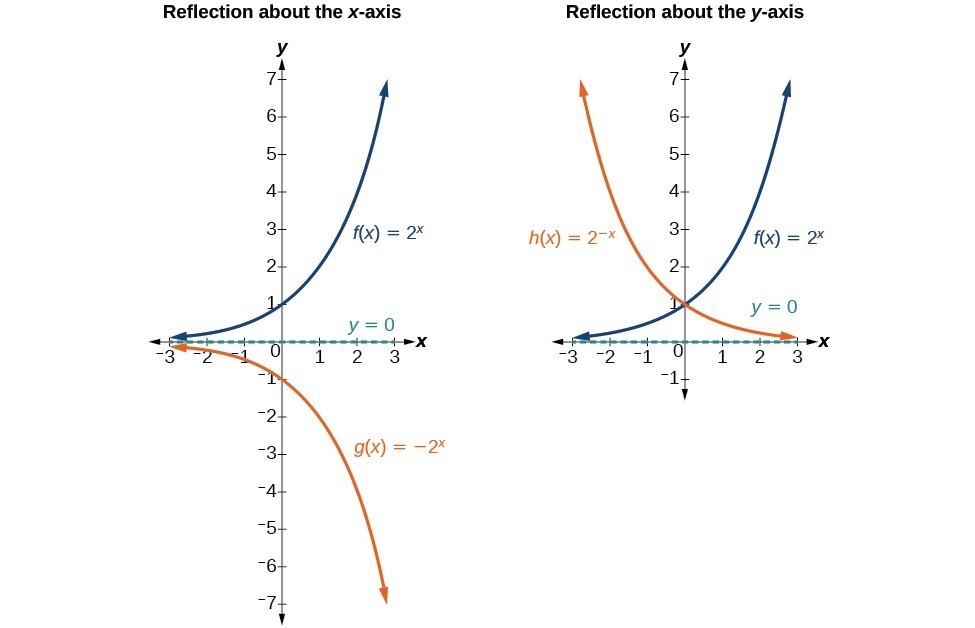


Graph Exponential Functions Using Transformations Math 1314 College Algebra


College Algebra Symmetry
Free functions symmetry calculator find whether the function is symmetric about xaxis, yaxis or origin stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyNov 16, 14Free Online Scientific Notation Calculator Solve advanced problems in Physics, Mathematics and Engineering Math Expression Renderer, Plots, Unit Converter, Equation Solver, Complex Numbers, Calculation History reflection across the line y=x 0 3615 1Oct 18, 17(2,5)rarr(6,5) A good diagram for these types of questions is useful From the diagram we see the object point (2,5) is mapped to (x',y') by a reflection in the line X=2 we note (1) the ycoordinate is unaffected (2) for reflections the distance from the line of reflection to the object is equal to the distance to the image point a=22=4units so the image point is 4 units
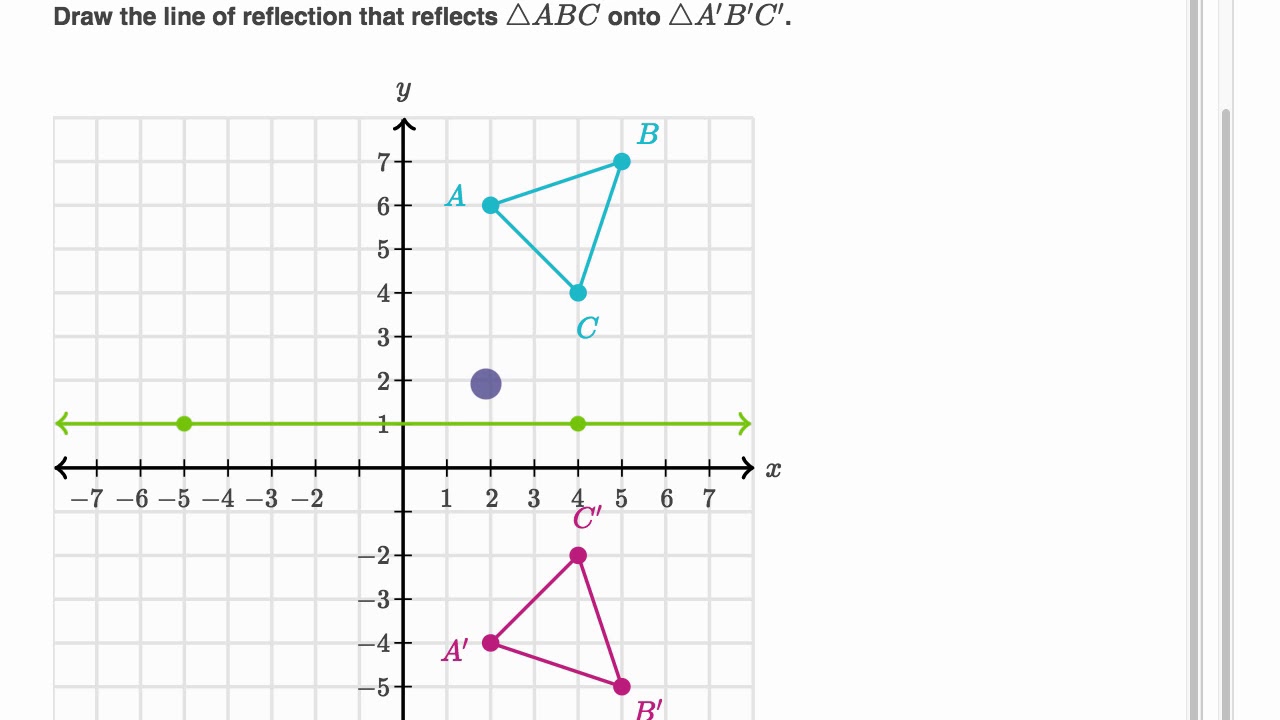


Line Of Reflection Example Youtube



Solved The Function F Defined By F X X2 Is Graphed In T Chegg Com
Reflecting across the line x = k (k is a constant);Point Reflection Calculator Point reflection, also called as an inversion in a point is defined as an isometry of Euclidean space It can also be defined as the inversion through a point or the central inversion Use our online point reflection calculator to know the point reflectionJun 24, In this manner, how do you calculate reflection?
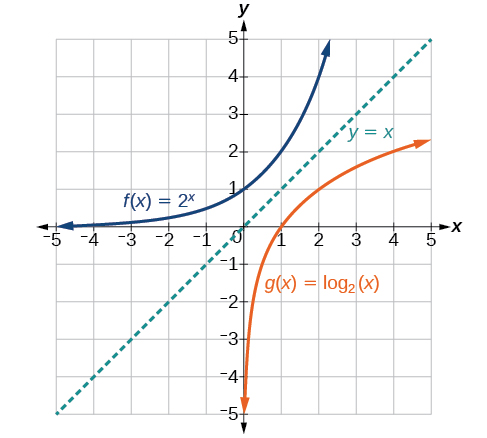


Graphs Of Logarithmic Functions Algebra And Trigonometry



Reflections Across Y X Geogebra
For a reflection over the x − axis y − axis line y = x Multiply the vertex on the left by 1 0 0 − 1 − 1 0 0 1 0 1 1 0A shape can be reflected in the line y = −x If point on a shape is reflected in the line y = −x both coordinates change sign (the coordinate becomes negative if it is positive and vice versa) the xcoordinate becomes the ycoordinate and the ycoordinate becomes the xcoordinateNov 10, 19Reflection over Y = X When a point is reflected across the line y = x, the xcoordinates and ycoordinates change their place Similarly, when a point is reflected across the line y = x, the xcoordinates and ycoordinates change their place and are negated Therefore, The reflection of the point (x, y) across the line y = x is (y, x) The
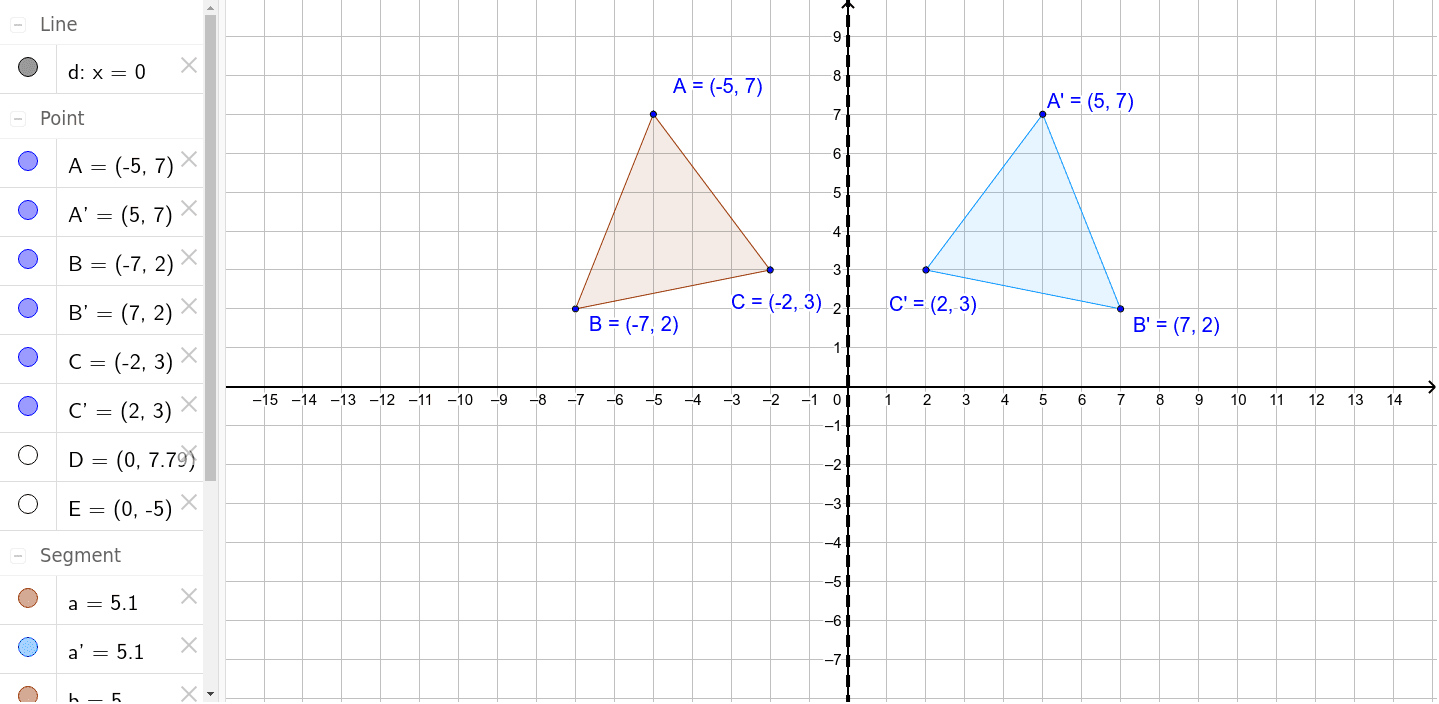


Reflection Over Y Axis Geogebra



How To Find A Reflection Image
→ Rgiven by a reflection across the line y=x А 60 (b) Find the matrix B of the linear transformation T R2 R?The ycoordinate changes, xcoordinate remains Reflecting across the line y = x;This set is called the axis (in dimension 2) or plane (in dimension 3) of reflection The image of a figure by a reflection is its mirror image in the axis or plane of reflection For example the mirror image of the small Latin
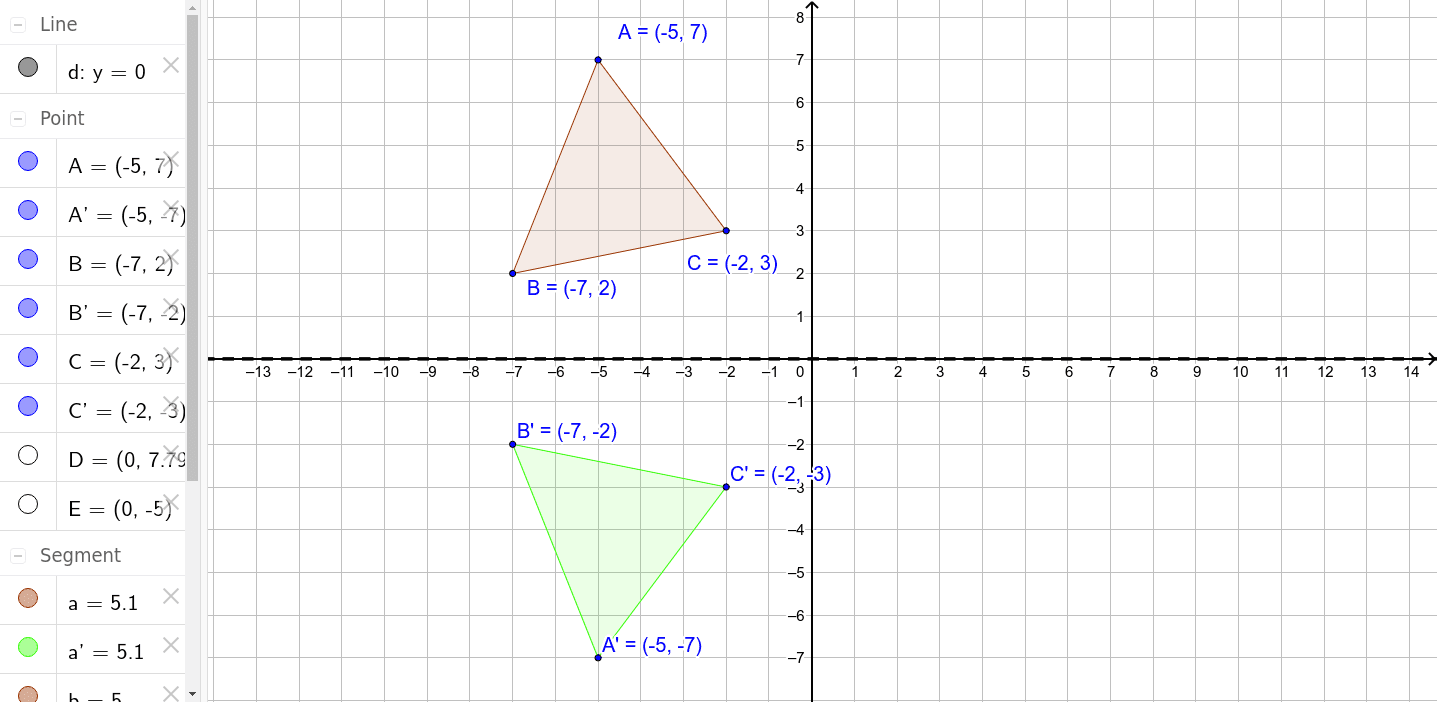


48 Reflection Over Y X Calculator Background Reflex



Scaling Reflecting Parabolas Video Khan Academy
Reflecting triangles across the Yaxis Loading Reflecting triangles across the Yaxis Reflecting triangles across the Yaxis Log InorSign Up First coordinate 1 A = Calculus Tangent Line example Calculus Taylor Expansion of sin(x) example Calculus Integrals example Calculus Integral with adjustable boundsA reflection is a flip over a line You can try reflecting some shapes about different mirror lines here How Do I Do It Myself?It's astonishing how difficult it is to find a good explanation how to reflect a point over a line that does not use higher math methods So here is my explanation You have a point \(P = (x,y)\) and a line \(g(x) = m \cdot x t\) and you want



Reflection Transformation Matrix



Erlang C Calculator Excel Including Shrinkage
Apr 29, 21A reflection can occur across any line, it is not limited to the three lines discussed previously The example below demonstrates a reflection that is not specific to the axes or the line y = x Examine the drawing below to see the relationship between theFree function shift calculator find phase and vertical shift of periodic functions stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept Number Line GraphReflection over the line y = − x A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the y
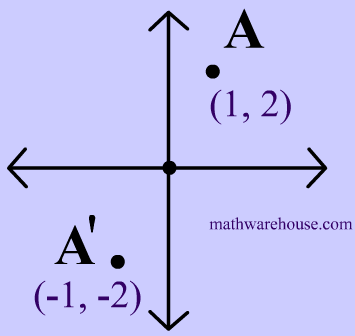


Point Reflections Formula And Examples Explained With Applet Examples And Practice Problems Center At Origin And At Any Arbitrary Point



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



The Rpa Interactive Calculator Download Scientific Diagram



Casio Fx ms 2nd Gen Non Programmable Scientific Calculator 240 Functions And 2 Line Display Amazon In Office Products
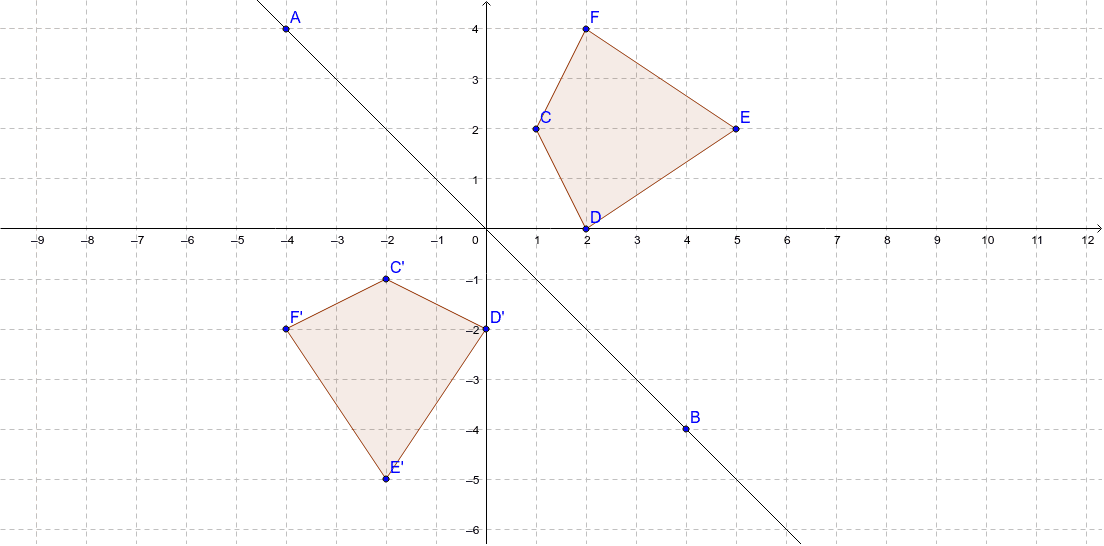


Reflection Over Y X Geogebra



3x3 Matrix Multiplication Calculator



Reflection Over The Line Y X Math Showme


Reflections Activity Builder By Desmos



Reflection Definition Reflection In The Coordinate Plane


Vector Projection Calculator



Graphing Cubed Root Functions Ck 12 Foundation



Reflection Rules How To W 25 Step By Step Examples



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines


Inverse Functions



Reflection Transformation Matrix



Solved Sketch The Graph Of The Function And Check The Gra Chegg Com
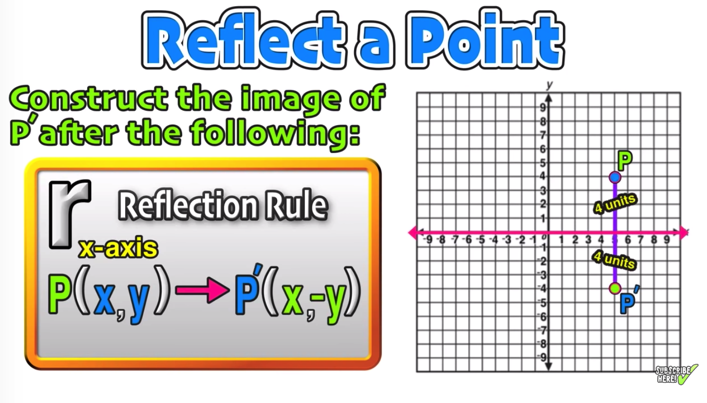


Reflection Over The X And Y Axis The Complete Guide Mashup Math
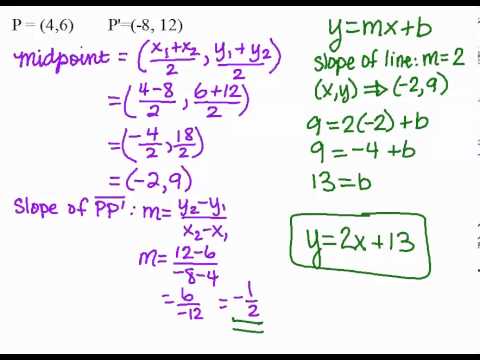


Writing The Equation Of A Line Of Reflection Youtube
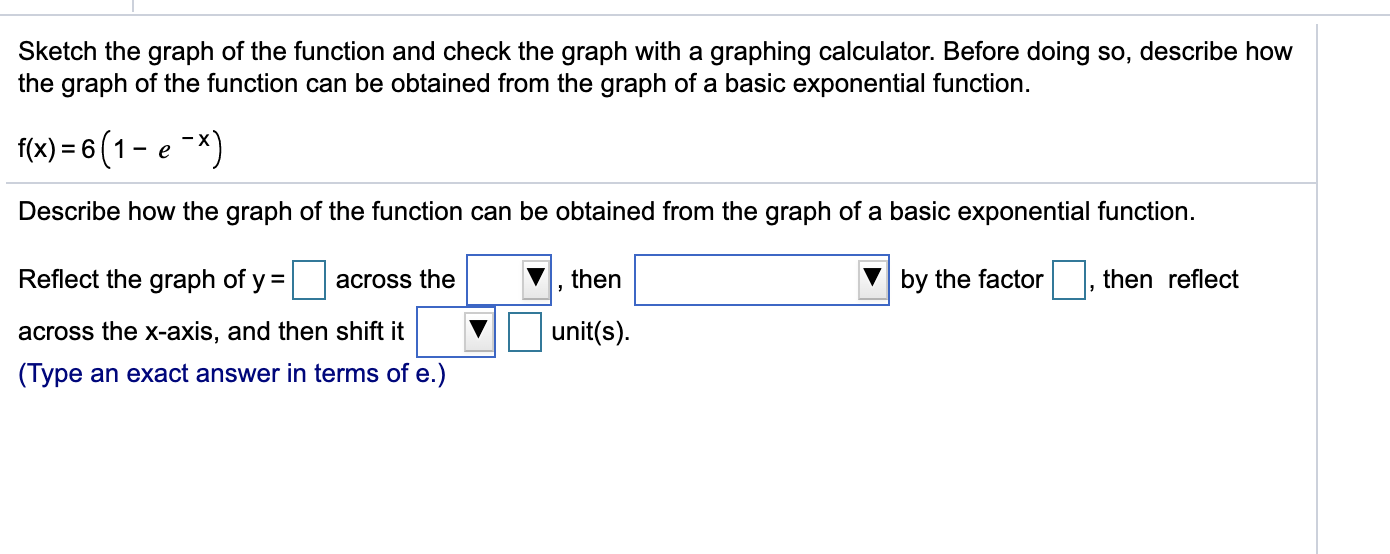


Solved Sketch The Graph Of The Function And Check The Gra Chegg Com



Reflection Mathbitsnotebook A1 Ccss Math
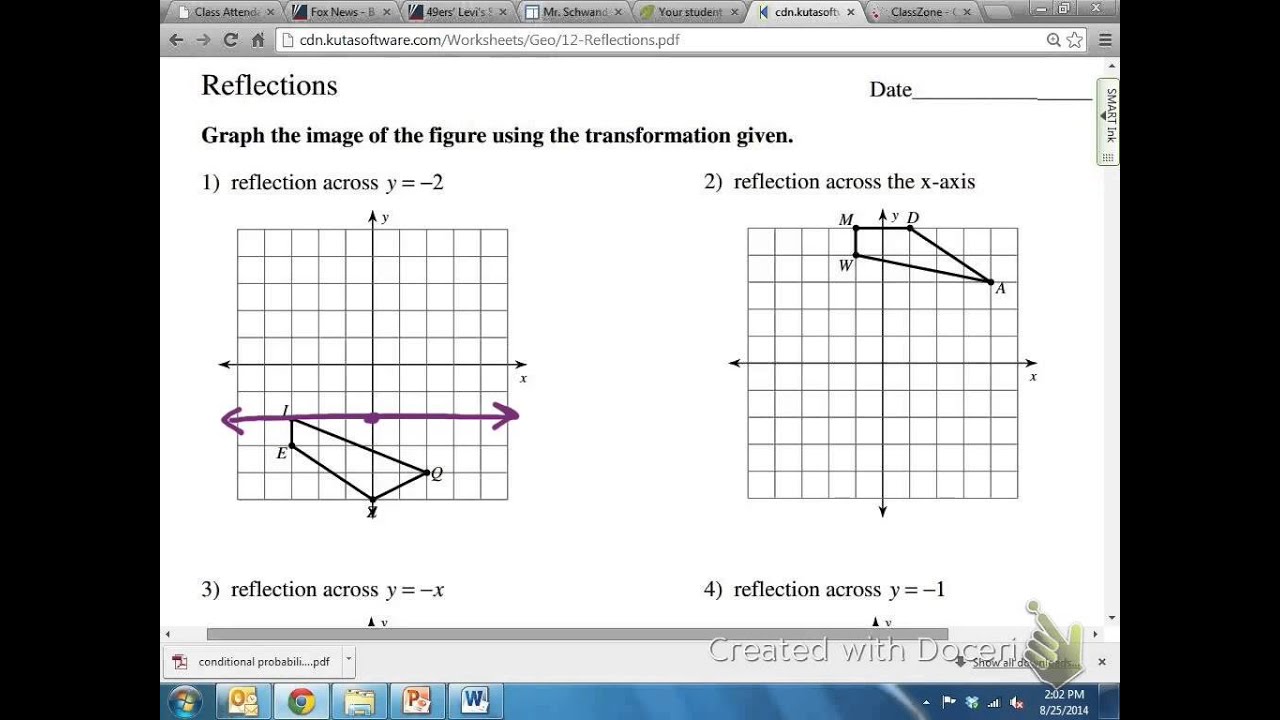


Common Core Math Geometric Reflection Over Y 2 Youtube
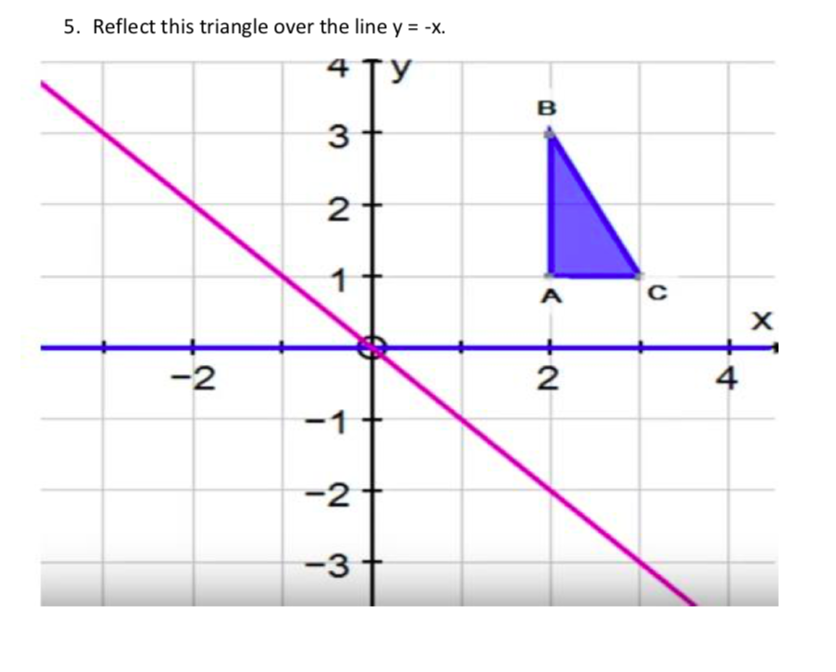


48 Reflection Over Y X Calculator Background Reflex



Answered Sketch The Graph Of The Function And Bartleby



Reflection Mathbitsnotebook A1 Ccss Math
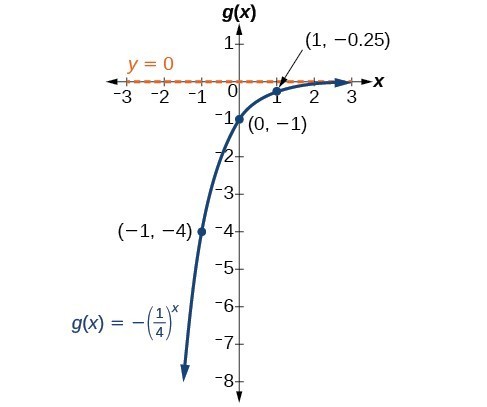


Graph Exponential Functions Using Transformations College Algebra



Act Math Practice Question 11 Answer And Explanation Crackact Com



Reflection



Reflection In The Line Y X Geogebra



Calculating Grease Quantity Frequency



View Question Parallelogram Abcd



Learn About Reflection Over The Line Y X Caddell Prep Online


College Algebra Symmetry


Reflection Across A Line Geogebra
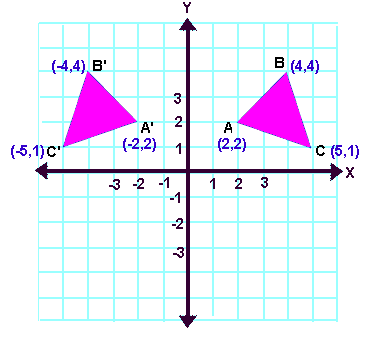


Reflection Transformation Matrix



Hwq 1 12 15 Evaluate The Definite Integral No Calculator Please Ppt Video Online Download



Reflection Rules How To W 25 Step By Step Examples



Transformation Reflection Over The Line Y X Youtube



Reflection Rules How To W 25 Step By Step Examples



How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
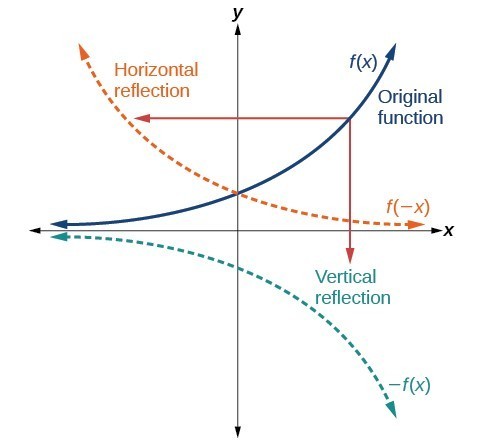


Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra



Reflection Mathbitsnotebook A1 Ccss Math



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



Casio Fx ms 2nd Gen Non Programmable Scientific Calculator 240 Functions And 2 Line Display Amazon In Office Products



How To Find A Reflection Image
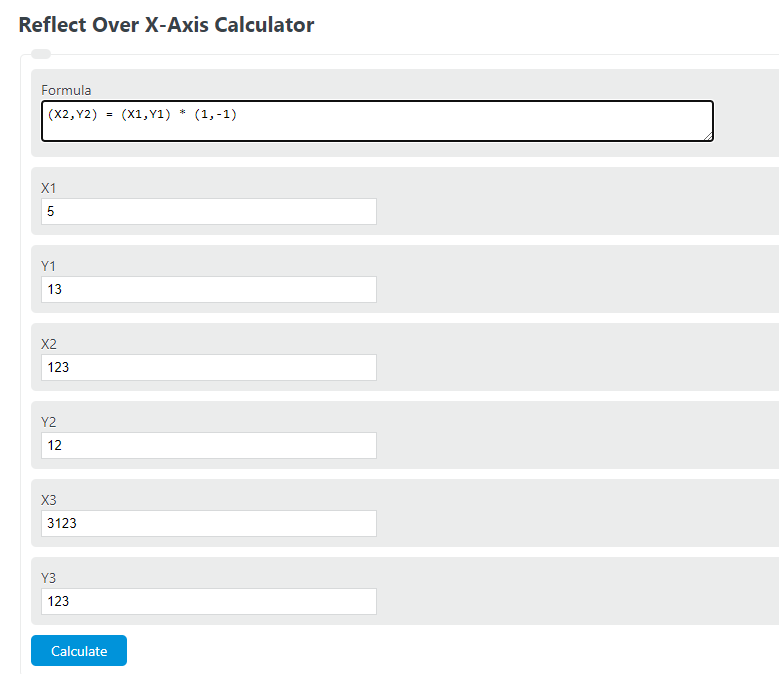


Reflect Over X Axis Calculator Calculator Academy



Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation


Aprmathb Transformations



Reflection Transformation Matrix
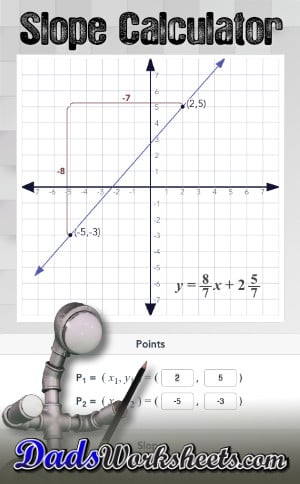


Slope Calculator
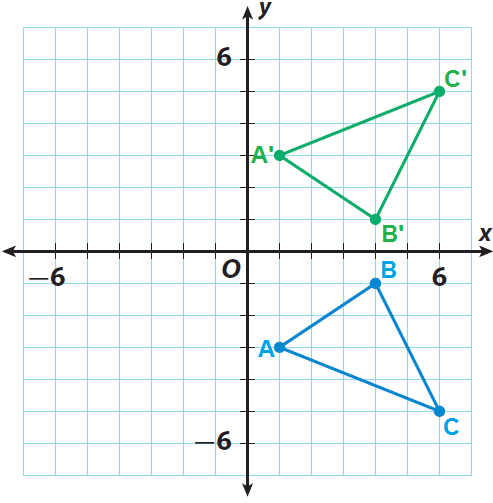


Algebraic Representations Of Reflections



Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation



How To Reflect A Graph Through The X Axis Y Axis Or Origin
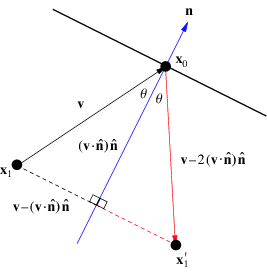


Reflection From Wolfram Mathworld



Reflecting Functions Introduction Video Khan Academy
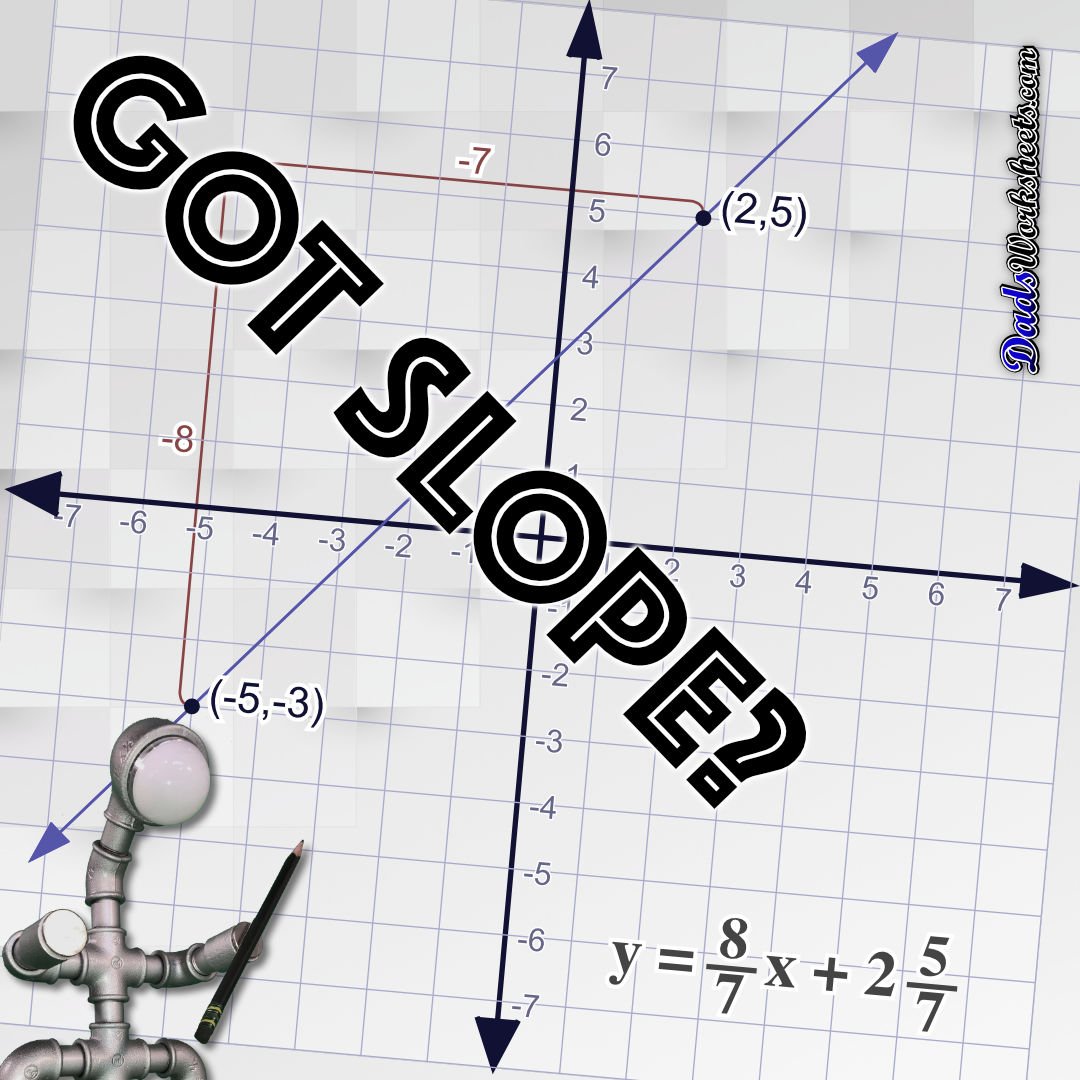


Slope Calculator
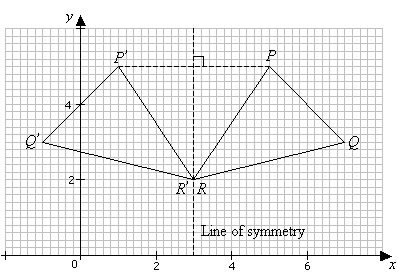


Reflection Transformation Solutions Examples Videos



Orthocenter Calculator Definition Formula



How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
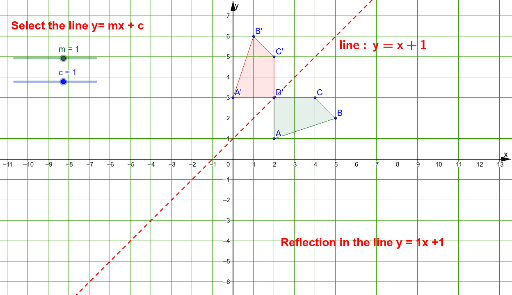


Reflections In The Line Y Mx C Geogebra



Casio Fx 991es Plus 2nd Edition Scientific Calculator Amazon In Office Products



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor



48 Reflection Over Y X Calculator Background Reflex
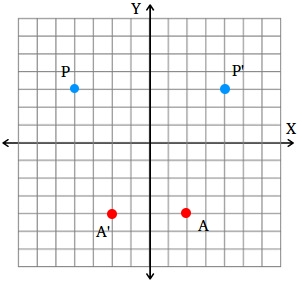


How To Find A Reflection Image


Solved Reflecting Across The Y Axis To Set Up This Activi Chegg Com



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor


View Question Reflection Across The Line Y X


